본 게시글은 "Competitive Programmer's Handbook"을 보며 임의로 해석하며 공부한 내용입니다.
알고리즘에서 그래프를 나타내는 몇가지 방법이 있다.
데이터 구조의 선택은 그래프 사이즈와 알고리즘이 동작하는 방법에 달려있다.
1. 인접 리스트 표현
- 노드 x개, 엣지 x개
그래프의 각 노드 x에는 x의 엣지가 있는 노드로 구성된 인접 리스트가 할당된다.
인접 리스트를 설계하는 방법은 벡터의 배열을 선언하는 것이다.
vector<int> adj[N];
예를 들어, 아래의 그래프는 다음과 같이 설계할 수 있다.

adj[1].push_back(2); // 1 > 2
adj[2].push_back(3); // 2 > 3
adj[2].push_back(4); // 2 > 4
adj[3].push_back(4); // 3 > 4
adj[4].push_back(1); // 4 > 1
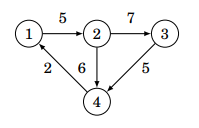
가중치 그래프는 다음과 같이 선언한다.
vector<pair<int, int>> adj[N];아래의 그래프는 다음과 같이 설계한다.

// pair(node, weight)
adj[1].puch_back({2,5});
adj[2].puch_back({3,7});
adj[2].puch_back({4,6});
adj[3].puch_back({4,5});
adj[4].puch_back({1,2});
인접 리스트 사용의 이점은 특정 노드에서 엣지를 통해 이동할 수 있는 노드를 효율적으로 찾을 수 있다는 점이다.
예를 들어, 다음 코드는 노드에서 이동할 수 있는 모든 노드를 거친다.
for (autu u : adj[s]) {
// process node u
}
2. 인접 매트리스 표현
- 엣지가 있는지? 없는지?
인접 매트릭스는 그래프에 포함된 엣지를 나타내는 2차원 배열입니다.
두 노드 사이에 엣지가 있는지 인접 매트릭스에서 효율적으로 확인할 수 있습니다.
int adj[N][N];
여기서 각 값 adj[a][b]는 그래프에 노드 a에서 노드 b까지의 엣지가 포함되어 있는지 여부를 나타낸다.
엣지를 그래프에 포함하면 adj[a][b] = 1이고, 그렇지 않으면 adj[a][b] = 0이다.
그래프를 표로 나타내면 다음과 같다.
 |
 |
만약 가중치 그래프라면,
 |
 |
인접 매트릭스 표현의 단점은 매트릭스가 n2 요소를 포함하며, 대부분 0이라는 것이다.
이러한 이유로 그래프가 클 경우 표현을 사용할 수 없다.
3. 엣지 리스트 표현
엣지 리스트에는 그래프의 모든 엣지가 순서에 따라 포함된다.
알고리즘이 그래프의 모든 엣지를 처리하고, 주어진 노드에서 시작하는 에지를 찾을 필요가 없는 경우 그래프를 표시하는 편리한 방법이다.
vector<pair<int, int>> edges;
pair(a, b)는 노드 a 에서 노드 b로의 엣지를 나타낸다.

edges.push_back({1,2});
edges.push_back({2,3});
edges.push_back({2,4});
edges.push_back({3,4});
edges.push_back({4,1});
만약 가중치 그래프라면,
vector<tuple<int, int, int>> edges;form(a, b , w)로 나타내면 마지막에 가중치를 추가해준다.

edges.push_back({1,2,5});
edges.push_back({2,3,7});
edges.push_back({2,4,6});
edges.push_back({3,4,5});
edges.push_back({4,1,2});'알고리즘' 카테고리의 다른 글
| [CSES] Coin Combinations I (0) | 2021.07.21 |
|---|---|
| [CSES] Minimizing Coins (0) | 2021.07.21 |
| [BOJ/백준] 1904번 - 01타일 (0) | 2021.07.11 |
| [BOJ/백준] 9461번 - 파도 (0) | 2021.07.09 |
| [BOJ/백준] 11399번 - ATM (0) | 2021.07.02 |

